Chapter 0. 선 요약
의사결정 나무 (Decision Tree)
1. 알고리즘의 원리, 개념
➔ 정보 전달량이 가장 높은 변수와 기준으로 split (트리 구조)
➔ 정보전달량 = 부모의 불순도 - 자식의 불순도
➔ 불순도 계산방법: 지니, 정보엔트로피
2. 전제조건
➔ NaN 조치, 가변수화
3. 성능 : hyper parameter, 복잡도 결정 요인
➔ max_depth : 클수록 모델이 복잡
➔ min_samples_leaf : 작을수록 모델이 복잡
세상에는 크게 3가지의 알고리즘군이 있다고 한다.
1. 딥러닝 (이미지, 자연어, 이상탐지 ...)
2. 베이지안
3. 트리기반 앙상블
그 기반이 되는 결정트리에 대하여
Chapter 1. Decision Tree
Tree 기반 알고리즘
➔ 특정 항목(변수)에 대한 의사 결정(분류) 규칙을 나무의 가지가 뻗는 형태로 분류해 나가는 분석 기법
• 분석 과정이 직관적이고 이해하기 쉽다.
• 분석 과정을 실제로 눈으로 관측할 수 있기 때문에 대표적인 화이트박스 모델
• Regression / Classification
• 계산 비용이 낮아 대규모의 데이터 셋에서도 비교적 빠르게 연산이 가능 (성능이 준수)
1. 정보의 전달
어떤 변수가 타겟 변수에 대한 중요한 정보를 담고 있는지 어떻게 알 수 있을까?
ex) 이동통신 가입고객의 이탈여부에 가장 큰 영향을 주는 변수는?
| 이탈여부 | 대학졸업 | 소득 | 가입기간 | 단말기 가격 | 월평균 초과비용 |
월평균 잔여시간 |
평균 통화시간 |
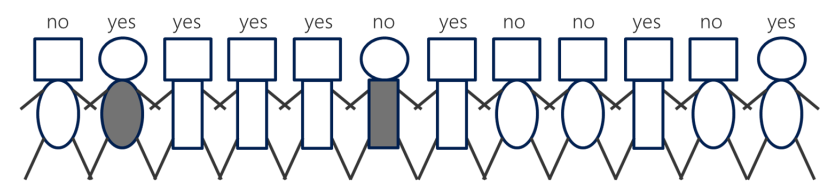
(그림 설명)
12명의 회원 중 이탈한 회원의 특징을 알아내려고 한다.
머리 위 yes, no는 이탈여부를 나타내는 타겟 변수.
속성 : 머리모양, 몸통 모양, 몸통색깔
어떤 속성이 타겟 변수에 대한 중요한 정보를 담고 있을까?

➔ 몸통모양을 기준으로 분류 ( 네모 : yes , 타원: no )
➔ 이를 수치화 해서 측정
• 순도(Pure Measure)
• 불순도 : 정보 엔트로피, 지니 계수
• 불순도에 기반한 정보 증가량을 측정
2. 지니 불순도(Gini Impurity)
➔ 분류 후 얼마나 잘 분류했는지 평가하는 지표
➔ 얼마나 순도가 증가했는지, 불순도가 감소했는지

위 그림에서 지니계수를 구해보면,

이 둘을 합쳐야 하는데, 이때 가중평균을 사용한다
➔ (이탈한 사람) / 전체 * 네모
+
➔ (이탈하지 않은 사람) / 전체 * 타원
전체 중의 비율로 곱한 다음 더하는 가중평균
지니 계수는 = 불순도(부모) – ( p(자식1) * 불순도(자식1) + p(자식2) * 불순도(자식2) + …)
불순도를 가장 많이 떨어뜨리는 변수가 가장 영향력 있는 변수 ➔ 위 그림에서는 몸통 변수
3. Tree 기반 모델링①
➔ 정보증가량이 가장 높은 속성을 첫번째 분할 기준으로 삼음
➔ 위 그림에선 [몸통] 변수


➔ 위와 같은 방식으로 트리는 점점 깊어지며 복잡해짐
➔ 트리의 크기(max_depth)에 따라 예측 결과(정확도)가 달라짐
➔ 말단 노드(leaf)까지 내려가면 train 데이터가 존재
➔ 말단노드에 위치한 train 데이터를 보고 중요한 변수들을 판단할 수 있음
4. Hyper parameter
➔ max_depth : 트리의 깊이(크기를 결정)
(max_depth가 깊을수록 복잡한 모델)
(depth는 경로의 길이와 동일)
➔ min_samples_leaf : leaf 노드의 최소 데이터 건수
(min_samples_leaf 가 작을수록 복잡한 모델)
(나뭇잎이 많으면 큰 나무)
(leaf 노드의 최소 데이터 건수의 디폴트 값은 1)
(그래서 조정없이 가만히 두면 가장 복잡한 모델을 생성한다)
(그러나, 복잡하다고 성능이 좋은 모델은 아니다) (오캄의 면도날)
(leaf 노드는 y를 예측하는데 사용되는데, 데이터가 적으면 예측 결과에 대해 신뢰도가 떨어질 수 있다.)
5. 결정트리의 시각화로 알 수 있는 것


① OverTime_Yes: (가변수화 한) [야근] 변수 ➔ 야근을 안함
(가변수화 시 변수의 값은 0 or 1) (0.5보다 작다는 것은 0이라는 의미)
② gini: 지니불순도(부모의 불순도)
③ samples: train 데이터의 개수
(데이터의 개수가 적으면 신뢰도가 떨어진다) (min_samples_leaf 로 조절)
④ value: 837개의 데이터 중 [701,106] ➔ [0]: 이탈x, [1]: 이탈o
⑤ class: 이탈x라고 판단
6. 변수 중요도
변수 중요도 생성 함수 코드
def plot_feature_importance(importance, names):
feature_importance = np.array(importance)
feature_names = np.array(names)
data={'feature_names':feature_names,'feature_importance':feature_importance}
fi_df = pd.DataFrame(data)
fi_df.sort_values(by=['feature_importance'], ascending=False,inplace=True) #중요도 순으로 정렬
fi_df.reset_index(drop=True, inplace = True)
plt.figure(figsize=(10,8))
sns.barplot(x='feature_importance', y='feature_names', data = fi_df)
plt.xlabel('FEATURE IMPORTANCE')
plt.ylabel('FEATURE NAMES')
plt.grid()
return fi_df이 함수를 이용해 변수 중요도를 시각화해 출력해보면
result = plot_feature_importance(model.feature_importances_, list(x_train))
➔ 결정 트리 모델에서 가장 상단에 위치한 변수는 [야근유무] 였는데 왜 그런 것일까? (그림에서는 6위)
➔ [야근] 변수는 부모의 불순도를 가장 많이 떨어뜨려 주는 변수 (가장 처음 split할 때 중요한 변수)
➔ 그러나, 모델 전체로 범위를 확장하는 순간 변수의 중요도는 평균으로 정렬됨
Tip)
1. <결정트리를 조정하는 법>
- 가지치기 (복잡)
- 생성부터 제한 (sklearn에서 주로 사용)
'KT-Aivle School (AI) > 머신러닝' 카테고리의 다른 글
| [모델링심화] 1. 성능 (0) | 2022.08.26 |
|---|---|
| [모델링기초] 5. SVM (0) | 2022.08.26 |
| [모델링기초] 3. 분류모델 (0) | 2022.08.24 |
| [모델링기초] 2. K-최근접이웃 (K-Nearest Neighbors) (0) | 2022.08.24 |
| [모델링기초] 1. 선형회귀 (0) | 2022.08.23 |