Chapter 0. 선요약
KNN
1. 알고리즘의 원리, 개념
➔ 거리를 계산하는 알고리즘 (스케일링이 필요)
➔ 학습데이터와 예측해야할 데이터의 거리를 계산하여 가까운 k 개 이웃의 label을 확인하고 나서 평균으로 예측
(이웃은 Train Data에서 찾음)
2. 전제조건
➔ NaN 조치, 가변수화, 스케일링(필수)
3. 성능 : hyper parameter, 복잡도 결정 요인
➔ k 값이 클수록 단순한 모델. 작을 수록 복잡한 모델
(K값은 최대로 train의 개수만큼 올릴 수 있으나, 이 모델은 평균모델과 동일하다.)
➔ 거리계산법에 의해서도 성능이 달라짐
(거리계산법에는 유클리드와 맨하탄이 있다.)
Chapter 1. K-Nearest Neighbors (KNN)
KNN
KNN은 거리를 계산하여 예측하는 '기본 알고리즘'
K개의 가까운 이웃에게 물어보는 알고리즘이라고 생각하면 쉬움
KNN의 절차
1) 예측해야 할 데이터 .predict(x_val) 와 주어진 데이터 train 의 모든 거리를 계산
2) 가까운 거리의 이웃 데이터 (train) 를 K개 만큼 찾은 후
3) K개 값(y)의 평균을 계산하여 예측(k개 값의 class를 보고 예측)
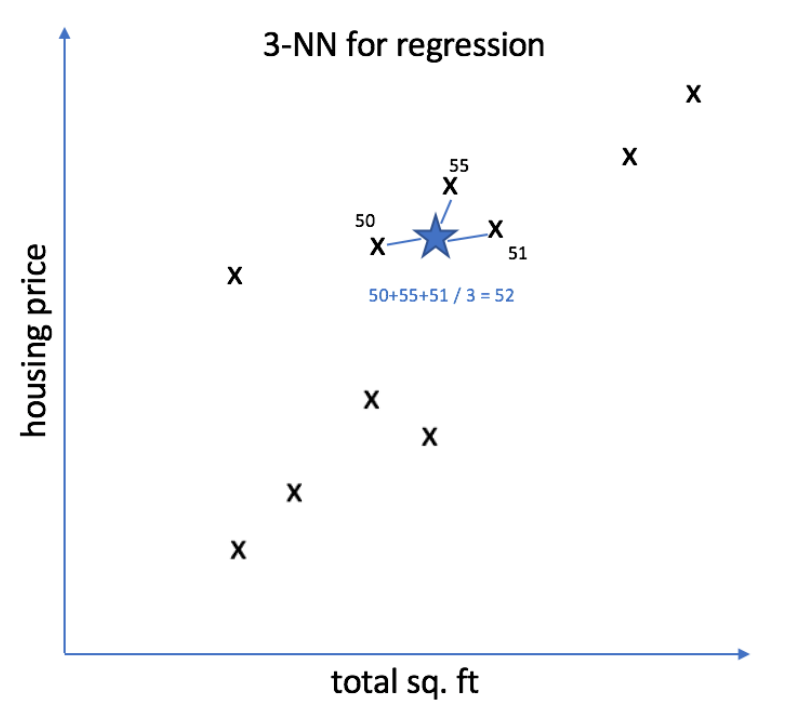
K값 결정
• K 에 따라서 예측 결과가 달라짐 ➔ 적절한 K값을 찾는 것이 목표
• K 값이 최대값일 때 예측 결과 ➔ 평균모델
• K 값이 1이면 ➔ 가장 가까운 데이터의 값
• K 값이 1이면 ➔ 보통 데이터 건수의 제곱근 근처에서 답을 찾으면 적당
KNN의 장점
1) 데이터의 분포 형태와 상관이 없다.
2) 설명변수(X)의 개수가 많아도 무리 없이 사용 가능
3) 괜찮은 성능
KNN의 단점
1) 계산시간이 오래 걸림 (최적화과정 없음)
2) 훈련데이터를 모델에 함께 저장 (모델사이즈가 커짐)
3) 해석하기 어려움.
KNN 알고리즘을 위한 거리계산법
1) Euclidean Distance
2) Manhattan Distance

KNN을 위한 전처리
1. Scaling (스케일링)
• Feature들 값의 범위와 단위가 각각 다름
• 값의 범위가 큰 Feature일 수록 거리 계산에 영향을 많이 준다.
• 그런 변수가 더 중요하게 여겨질 수 있다.
• 그러므로 모든 값의 범위를 맞춰 주는 것이 스케일링!
ex)
'나이' 변수의 범위: 20세 ~ 60세
'급여' 변수의 범위: 3,000만원 ~ 1억원
각 변수에서 13칸을 이동한다고 가정했을 때, [20세-33세]와 [3000만원-3013만원]의 의미는 다름
두 변수의 범위를 모두 0 ~ 1로 맞춰주는 방식 등으로 범위를 바꾸는 것이 스케일링
스케일링의 종류
방법 1 : Normalization
입력변수 X가 [a, b] 범위라면(a=min, b=max)
𝑋𝑛𝑜𝑟𝑚 = 𝑥 − 𝑎 % 𝑏 − 𝑎
from sklearn.preprocessing import MinMaxScaler # 0~1 값으로 변환
scaler = MinMaxScaler() # 선언
x_train_s1 = scaler.fit_transform(x_train) # fit_transform: fit + transform = 기준을 찾고, 적용
x_val_s1 = scaler.transform(x_val) # 적용만MinMaxScaler: 변수의 범위를 0~1로 변환하는 스케일링
* .fit_transform(x_train)
. fit ➔ x_train의 변수별로 최대값과 최소값 (Min, Max)를 찾는 것
transform ➔ 적용

* transform(x_val)
transform ➔ Min과 Max는 train데이터를 기준으로 찾았으니 val 데이터에는 적용만
(validation 데이터는 검증용이므로 .fit된 train데이터 기준에 따라 스케일링을 해야함)
방법2 : Standardization
𝑋𝑧 = 𝑥 − 𝑚𝑒𝑎𝑛 % 𝑠𝑡d
모든 값의 평균과 표준편차를 0과 1로 변경 (mean = 0, std = 1)

. fit ➔ x_train의 변수별로 평균과 표준편차를 찾는 것
방법3 : MaxAbsScaler
최대절대값과 0이 각각 1, 0이 되도록 스케일링
방법4 : RobustScaler
중앙값(median)과 IQR(interquartile range) 사용. ➔ 아웃라이어의 영향을 최소화
Tip)
(1) 스케일링이 필요한 알고리즘: KNN, SVM, 딥러닝
(2) KNN 알고리즘에서 K의 값은 보통 데이터 건수의 제곱근 근처가 적당
'KT-Aivle School (AI) > 머신러닝' 카테고리의 다른 글
| [모델링심화] 1. 성능 (0) | 2022.08.26 |
|---|---|
| [모델링기초] 5. SVM (0) | 2022.08.26 |
| [모델링기초] 4. Decision Tree (0) | 2022.08.26 |
| [모델링기초] 3. 분류모델 (0) | 2022.08.24 |
| [모델링기초] 1. 선형회귀 (0) | 2022.08.23 |