Chapter 1. 학습 관련 기술들
최적화 방법
스토캐스틱 경사하강법(SGD)의 경우 단순하고 구현도 쉬우나, 비효율적일 때가 많다
(한 점마다 기울기를 측정하여 기울어진 방향으로 일정거리를 이동하니 기울기가 매번 달라지는 경우 경로가 비효율적)
이러한 SGD의 단점을 개선해주는 방법으로 '모멘텀, AdaGrad, Adam' 등이 있다.
Momentum
- 기본적으로 SGD와 유사하지만, 속도(v)라는 개념이 추가됨
- 즉, 물체가 아무런 힘을 받지 않을 때에도 서서히 하강시키는 역할을 수행함
AdaGrad
-신경망 학습에서 중요한 학습률(learning rate)을 서서히 낮추는 방법
- 개별 매개변수에 적응적으로(Adaptive) 학습률을 조정하면서 학습을 진행함
- 즉, 학습률 감소가 매개변수의 원소마다 다르게 적용됨
- 그러나 AdaGrad는 과거의 기울기를 제곱해서 계속 더하기 때문에, 학습을 진행할수록 갱신 강도가 약해져
무한히 계속 학습할 경우에는 어느 순간 갱신량이 "0"이 되어서 갱신이 이루어지지 않는 단점이 있음
* RMSProp
➜ 과거의 모든 기울기를 균일하게 더해가는 것이 아니라,
먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영(지수이동평균)함 (AdaGrad 개선)
Adam
- Momentum과 AdaGrad 방법을 결합한 방법임
- Adam 방법은 하이퍼파라미터의 편향 보정이 진행됨
- Adam은 하이퍼파라미터를 3개 설정함
➜ 학습률(learning rate) = alpha
일차 모멘텀용 계수 beta1 (default 값은 0.9)
이차 모멘텀용 계수 beta2 (default 값은 0.999)
일반적으로 SGD보다 위의 세 기법이 빠르게 학습하고, 최종 정확도도 높게 나타난다.
배치 정규화 (Batch Normalization)
신경망 학습의 핵심 중 하나는 '가중치의 초깃값을 무엇으로 설정하느냐'다.
가중치의 초깃값을 적절히 설정하면 각 층의 활성화 값 분포가 적당하게 퍼져 학습이 원활하게 수행된다.
반대로 분포가 다른 경우 학습을 방해하는데, 이러한 현상을 Internal Covariate Shift라고 한다. (학습이 불안정)
학습이란, 에러를 줄이는 방향으로 가중치를 업데이트 하는 것.
스케일링 레이어가 없다면, 레이어가 깊어질수록 분산형태가 바뀜
(학습시키는 데이터가 달라지면 분포도 바뀔수 있음)
딥러닝에서 층에서 층으로 이동될 때마다 이전 층의 학습에 의해 가중치 값이 바뀌게 되면
현재 층에 전달되는 입력 데이터의 분포와 현재 층에 학습했던 시점의 분포와 차이가 발생
이렇게 층 별로 입력 데이터 분포가 달라지는 현상을 Internal Covariate Shift (내부 공변량 변화)라고 한다.

하지만, 이렇게 초깃값을 잘 설정하는 것은 매우 어려운데,
각 층의 활성화 값 분포가 적당히 퍼지도록 강제로 만든다면 간단해진다.
이것이 Batch Normalization이다.
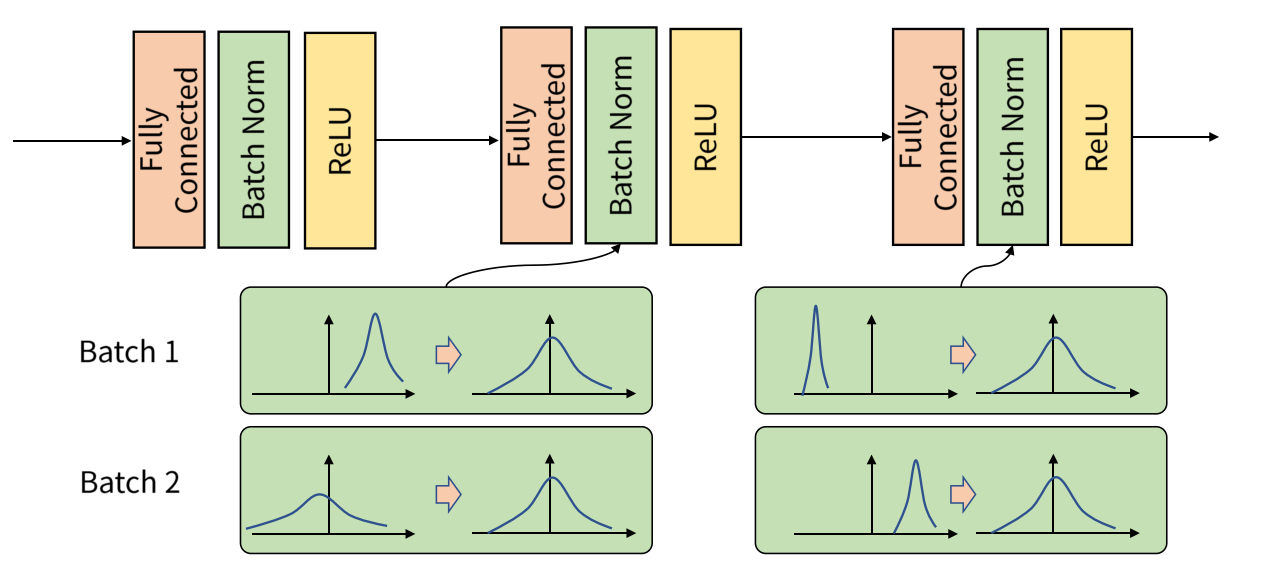
Batch Nomalization
- 신경망의 순전파 때 적용, 각 층에서 활성화 값이 적당히 분포되도록 강제로 조정
➜ (학습 시 미니배치를 단위로 정규화를 수행)
- 쉽게 말해, Batch별로 스케일링 적용
➜ (데이터의 분포가 평균이 0, 표준편차가 1이 되는 정규분포를 따르도록 정규화)
장점
- 학습 속도가 빨라짐
- 가중치 초깃값 의존도 감소
- 오버피팅 억제
DropOut
train데이터에 대한 정확도는 높으나 test데이터에 대한 정확도는 낮은 것을 Overfitting이라고 한다.
과적합(Overfitting)은 주로 아래와 같은 이유로 발생한다.
- 매개변수가 많고 복잡한 모델
- 학습 데이터가 적은 경우
DropOut은 과적합을 억제하는 대표적인 방법 중 하나이다.
드롭아웃(Dropout)
- 신경망 모델이 복잡해지면 가중치 감소(Weight Decay)만으로는 과적합 문제를 해결하기가 어려움
- 드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법
➜ 즉, 학습할 때 은닉층의 뉴런을 무작위로 골라서 삭제하고, 삭제된 뉴런은 신호를 전달하지 않게 됨
(의도적으로 히든 레이어 속 노드를 제거 ➜ 과적합 방지)
학습할 때는 데이터를 흘릴 때마다 삭제할 뉴런을 무작위로 선택하지만,
테스트할 때는 모든 뉴런에 신호를 전달한다는 점을 주의.
단, 테스트할 때는 각 뉴런의 출력에 학습할 때 삭제 안 한 비율을 곱해서 출력함.

Chapter 2. CNN
Computer Vision의 목표는 '컴퓨터가 이미지를 이해하게 하는 것'
그러나, 컴퓨터에게 시각지능을 갖게 하기는 매우 어렵다.
그래서 고안해낸 방법 중 하나가 컴퓨터에게 경계(외곽선)을 가르쳐 보자는 것
값이 급격히 변화하는 곳이 ➜ 경계
미분을 이용하여 값이 급격하게 변화하는 곳을 모두 찾아 연결하면 경계를 찾을 수 있었다.
(단, 흑백에서만 가능)
그러나, 컬러사진이라면?
➜ 예외상황이 너무 많고, 찾은 경계에는 종종 노이즈가 존재했다
+
각도, 빛에 따라서 이미지(데이터)역시 달라짐
Object Detection은 먼나라 이야기, Edge Detection 조차 쉽지 않음
합성곱 신경망 (Convolutional Neural network,CNN)
이미지를 이미지답게 다뤄내는 최초의 알고리즘
CNN은 이미지를 인식하고 처리하는 CV분야에서 현재까지도 인기있는 신경망 모델이다.
얀 르쿤(Yann Lecan) 교수는 인접한 두 층의 노드들이 전부 연결 되어있는 기존의 인공신경망이 아닌
특정 국소 영역에 속하는 노드들의 연결로 이루어진 획기적인 인공신경망을 고안해 냈다.
이것이 바로 합성곱 신경망(Convolutional Neural Network, CNN) 이다.

CNN은 입력으로 받은 고양이 사진을 필터링과 분류의 과정을 거쳐 '고양이'라고 출력한다.
이때, 필터링을 거친 원본 데이터를 Feature map이라고 하며,
필터를 어떻게 설정할지에 따라 피처맵이 달라지므로
CNN에서 학습시켜야 할 대상은 바로 필터(= Kernel)가 된다.
특징 맵(Feature Map)
합성곱 계층의 입/출력 데이터를 의미함입력 데이터는 입력 특징 맵(Input Feature Map)
출력 데이터는 출력 특징 맵(Output Feature Map)이라고 함
입력 데이터인 이미지는 대게 (높이, 너비, 채널)로 구성된 3차원의 데이터로
여기서 채널이란 이미지가 가진 색상을 표현하기 위해 필요한 적(red), 녹(green), 청(blue)을 뜻한다.
컬러 사진은 3개의 채널을 가지며 참고로 흑백 사진은 채널이 1 이므로 2차원의 데이터가 된다.
기존에 등장했던 신경망인 완전 연결 신경망의 경우, 3차원의 이미지 데이터를 학습시키기 위해 1차원으로 평면화 시키는데 이 과정에서 이미지의 공간 정보가 유실이 되게 된다.
이미지의 공간 정보란 말 그대로 이미지가 가지는 ‘공간적인 정보’를 말한다.
이미지를 이루는 가장 작은 단위를 픽셀(pixel)이라고 하는데 거리가 가까운 픽셀들은 서로 연관을 띠게 된다.
이는 곧 사진에서 음영, 선, 질감 등으로 보여지는 것이며
다시 말하면 이런 픽셀들의 연관성이 이미지가 가지는 공간정보라고 할 수 있다.
CNN은 입력 데이터의 원래 구조를 유지해서 입력 받고 다음 단계로 전달할때에도 이 구조를 유지한다.
합성곱 연산
CNN의 첫번째 단계는 필터링 과정이다.
➜ 입력 받은 이미지를 잘 분류하기 위해 이미지에 필터를 씌워 특징을 찾는 작업
➜ 합성곱 연산이라고 하는 계산을 통해 이루어짐
이미지 처리에서 말하는 필터 연산에 해당
합성곱 연산을 위해서는 입력 데이터와 필터가 필요하다.
사이즈는 (높이, 너비)로 표현하며 필터는 주로 (3,3)과 같은 정방행렬을 사용한다.
(CNN의 학습 대상은 필터의 값(weight)이므로 적절한 초기 값을 설정할 필요가 있다.)

위 그림은 입력 데이터(4,4) * 필터(3,3) 의 합성곱 연산을 나타내는 그림이다.
합성곱 연산은 필터의 윈도우(window)를 일정 간격으로 이동해가며 입력 데이터에 적용한다. (회색 부분)
먼저 위 그림과 같이 입력 데이터와 필터에서 대응하는 원소끼리 곱한 후에 그 총합을 구한다.
그리고 나서 그 결과를 출력의 해당 장소에 저장하는 방식으로 연산이 이루어진다.
위 그림에서는 생략되어 있지만 CNN에서 편향(bias)까지 고려한다면 아래와 같이 연산을 수행한다.

위 그림에서 마지막으로 출력된 특성 맵은 채널이 하나인 흑백 사진이다.
이 과정을 세개의 채널(RGB)에 적용한 컬러 이미지의 경우 (높이, 너비, 채널)의 크기를 가지며 피처맵이 도출되는 과정은 아래의 그림과 같다.

합성곱 연산을 세개의 채널에 각각 적용한 뒤에 얻은 결과 값을 같은 위치의 원소끼리 더하기만 하면(element-wise sum)
3차원의 컬러 이미지에 대한 피처맵을 얻을 수 있다. 이 과정을 입체적으로 보면 다음과 같다.

위 그림을 보면 원본 이미지에 필터를 한번만 적용해도 원래의 이미지 보다 절반이나 작아진 것을 볼 수 있다.
앞에서 합성곱 연산은 원본 이미지의 특징을 찾기 위해 필터를 씌우는 과정이라고 했다.
그러나 피처맵의 계속 작아져 (1,1) 사이즈가 된다면 더이상 합성곱 연산을 적용하지 못하게 된다.
이런 출력 크기 문제를 보완하기 위해 등장한 기법이 바로 패딩(padding)이다.
패딩 (Padding)
합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정 값(일반적으로 "0")으로 채우기도 하는데,
이를 패딩(Padding)이라고 하며 합성곱 연산에서 자주 이용하는 기법이다.

패딩은 '충전재'라는 의미처럼 입력 데이터를 특정 값으로 둘러싸는 것을 말한다.
일반적으로 특정 값은 0을 사용하기때문에 zero-padding이라고도 한다.
아래 이미지는 (4,4)인 입력데이터에 폭이 1 픽셀인 제로 패딩을 적용하여 입력데이터가 (6,6)이 된 이미지다.

세임 패딩 (same padding) (=half padding)
패딩(Padding)은 주로 출력 크기(Output Size)를 조정할 목적으로 사용된다. (원소들이 골고루 고려되도록)
세임패딩을 적용한 경우, 원본 데이터의 크기와 같은 피처맵을 출력할 수 있다.
(데이터의 공간적 크기를 고정한 채로 다음 계층에 전달)
세임 패딩은 출력 크기를 입력 크기와 동일하게 유지한다.
입력데이터 (Hi,Wi) 와 (F, F) 사이즈의 필터가 있을때 세임 패딩의 폭 P는 (F-1)/2가 된다.
그러므로 세임 패딩을 적용한 입력 데이터의 크기는 (Hi+2*P, Wi+2*P)가 된다.
이처럼 세임 패딩은 풀패딩의 절반 개념이므로 절반 패딩(half padding) 라고도 부른다.
(+추가)
밸리드 패딩 (valid padding): 패딩을 추가 하지 않은 형태
밸리드 패딩을 적용하고 필터를 통과시키면 그 결과는 항상 입력 사이즈보다 작게 된다.
밸리드 패딩은 입력데이터의 모든 원소가 같은 비율로 사용되지 않아 모서리의 정보가 과소평가된다.
풀 패딩 (full padding): 입력데이터의 모든 원소가 합성곱 연산에 같은 비율로 참여하도록 하는 패딩 방식
패딩 이외에도 원소별 연산 참여 횟수를 조절하는 것이 있다.
스트라이드 (stride)
스트라이드(Stride, 보폭)란 필터를 적용하는 위치의 간격이다.
아래의 그림은 스트라이드가 2인 합성곱 연산의 예시인데, 그림을 보면 알 수 있듯이 윈도우(Window)가 두 칸씩 이동하는 것을 알 수 있다.

스트라이드(Stride)를 크게 설정하면 출력 크기(Output Size)는 작아진다.
(디폴트는 1)
특징 맵(Feature Map), 필터(Filter = Kernel), 패딩(Padding), 스트라이드(Stride) 사이의 관계
수식으로 나타내면 아래와 같다.


(+ 예제)
입력데이터 (10, 10), 필터 (3, 3), 패딩 폭 P = 2, 스트라이드 S=1 일때 출력데이터 (Ho,Wo)의 크기는?
= (12,12)
풀링 층 (Pooling Layer)
풀링층은 가로*세로 방향의 공간을 줄여 피처맵의 크기를 작게만들어 신경망의 계산량을 줄이는 기법
목적: subsampling
합성곱 층에서 최종적으로 얻은 피처맵은 ReLu를 적용해 값을 산출하여 풀링층으로 전달되고
풀링 층의 입력으로 들어가면 크기가 작아져서 반환된다.
풀링 연산은 채널마다 독립적으로 작동 ➜ 채널의 수가 변하지 않음
풀링은 입력 데이터의 영역별로 하나의 원소를 뽑는다.
뽑는 기준은 최대값, 최소값, 평균 값이 있으며
이를 순서대로 최대 풀링(Max pooling), 최소 풀링(Min pooling), 평균 풀링(Average pooling)이라고 한다.

- 최대 풀링은 영역별로 가장 중요한 특징을 추출
(가장자리(edge)나 질감(texture)와 같은 이미지의 구조를 포착하는데 유용하므로 이미지 인식 분야에서 많이 사용)
- 평균 풀링은 영역의 모든 값들을 고려하여 평균 값을 내므로 매우 부드러운 특징을 추출
그리고 풀링(Pooling)의 윈도우(Window) 크기와 스트라이드(Stride)는 같은 값으로 설정하는 것이 일반적이다.
Flatten
하나의 이미지로부터 다양한 특이점들을 뽑아내고 이것을 1차원의 데이터로 변형하는 것.
Convolution과 Pooling을 반복하면 이미지의 숫자는 많아지면서 크기는 점점 줄어든다.
- 즉, 최종적으로 도출된 nxn 이미지는 이미지라기보다는 특정 이미지에서 얻어온 하나의 특이점 데이터가 된다는 것.
- 즉, 2차원이 아닌 1차원의 row 데이터로 취급해도 무관한 상태가 된다는 의미
- Flatten 과정을 거친 후 DNN과 동일하게 만들어진 네트워크를 통해 OutPut 출력.

완전 연결 계층 (Fully Connected Layer)
합성곱층과 풀링층은 마치 한 묶음처럼 여겨져 CNN 속에서 여러번 반복 되어 사용된다.
(원본 이미지의 특징을 찾는 과정이므로)
입력데이터가 합성곱 층과 풀링층을 통과한 후 Flatten layer를 거쳐 수직으로 펼쳐진다.
수직으로 펼쳐진 Feature Map들은 완전 연결 계층의 입력으로 넣어진다.
완전 연결 계층에서는 이전까지의 과정을 통해 얻어진 원본 이미지의 특성들을 이용해 분류의 과정을 거친다.
그리고 마지막 출력층에서는 다중 출력에 사용되는 활성함수인 소프트맥스(softmax)를 사용해 최종 출력을 만든다.
아래 그림은 지금까지 정리한 CNN의 구조를 한 눈에 나타낸 것이다.

이렇게 CNN을 통해 합성곱이 레이어를 여러 겹 쌓으면서 층이 깊어지고 더 복잡하고 추상화된 정보가 추출된다.
즉, 층이 깊어지면서 뉴런이 반응하는 대상이 단순한 모양에서 "고급" 정보로 변화해간다는 뜻이다.

+ 추가)
Batch Normalization의 한계

- Batch Normalization은 Batch의 크기에 영향을 많이 받습니다.
- 만약 Batch의 크기가 너무 작으면 잘 동작하지 않습니다. 따라서 GPU 메모리의 한계로 인해 RNN이나 크기가 큰 CNN에 적용하기가 어렵습니다. 극단적으로 Batch 사이즈가 1이 되면 평균은 샘플 1개의 값이 되고 표준 편차는 0이 됩니다. 이렇게 되면 정상적으로 동작할 수가 없습니다.
- 또한 샘플을 너무 작게 사용할 때에는 큰수의 법칙과 중심 극한 이론을 만족하지 못하기 때문에 평균과 표준 편차가 데이터 전체 분포를 잘 표현하지 못하는 것을 알 수 있습니다.
- 반대로 Batch의 크기가 너무 커지는 경우에도 잘 동작하지 않습니다. 왜냐하면 적절한 크기의 샘플은 중심 극한 이론을 통하여 적절한 정규 분포를 따르게 되나 굉장히 큰 샘플을 한 경우 multi modal 형태의 gaussian mixture 모델 형태가 나타날 수 있기 때문입니다. (정규 분포의 봉우리가 여러개 나타나는 형태) 이와 같은 경우 단순히 평균과 표준 편차를 사용하는 것은 정확한 모델링이라고 말할 수 없습니다.
- 뿐만 아니라 Batch 크기가 너무 크면 병렬 연산 하는 데에도 비효율적일 수 있습니다.
- 또한 gradient를 계산하는 시점이 Batch 단위인데, gradient를 계산을 너무 한번에 하게 되어 학습에도 악영향이 있을 수 있습니다.
- 이러한 Batch Normalization의 한계를 개선하기 위하여 Weight Normalization이나, Layer Normalization 등이 사용되기도 합니다. 이 내용은 아래 링크를 참조하시기 바랍니다.
- 링크 : https://gaussian37.github.io/dl-concept-various_normalization/
* 참조
https://ardino.tistory.com/41?category=1094784
선생님, Padding은 뭔가요?(2) - 스트라이드 (Stride)
스트라이드는 사전적으로 ‘보폭’이라는 의미를 갖는다. 마찬가지로 입력데이터에 필터를 적용할때를 생각해보자. 아래의 예제는 앞에서 계속 다루었던 (4,4)사이즈의 입력 데이터에 (3,3) 필터
ardino.tistory.com
https://data-scientist-brian-kim.tistory.com/86
[밑바닥부터 시작하는 딥러닝 1] Ch 7. 합성곱 신경망(CNN)
이미지 인식 분야에서 딥러닝을 활용한 기법은 거의 다 합성곱 신경망(CNN)을 기초로 한다. 그렇다면 합성곱 신경망. 즉, CNN이란 무엇일까? 이번 포스팅에서는 CNN에 대해 정리해보도록 하겠다. CNN
data-scientist-brian-kim.tistory.com
'KT-Aivle School (AI) > 딥러닝' 카테고리의 다른 글
| [언어지능 딥러닝] 텍스트 마이닝 (0) | 2022.10.05 |
|---|---|
| [언어지능 딥러닝] NLP (자연어 처리) (2) | 2022.10.04 |
| [Computer Vision] Object Detection (0) | 2022.09.23 |
| 라이브러리 모음 (0) | 2022.09.19 |
| 딥러닝 기초 (0) | 2022.09.14 |