딥러닝 기초
Chapter 0. 선 요약
Chapter 1. 딥러닝
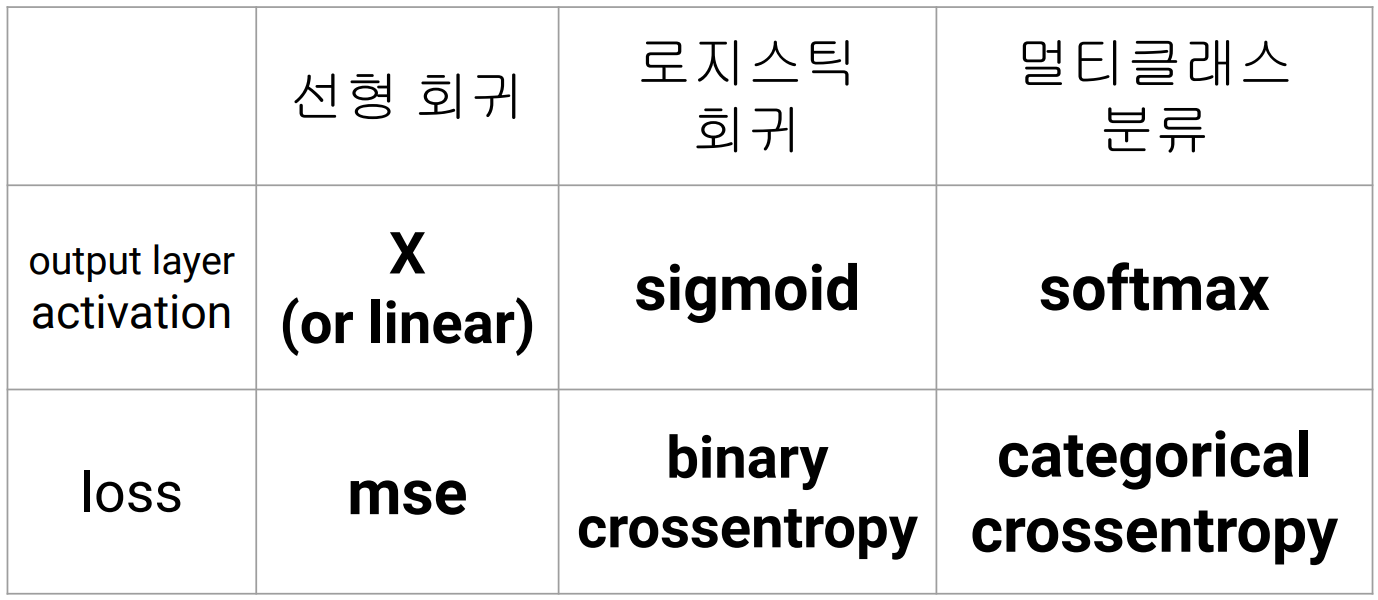
딥러닝과 머신러닝 구별

머신러닝: 수제작이기 때문에 주어진 데이터가 성능을 좌우한다
➜ 설명이 용이함 (성능만 좋다면)
➜ 오차를 줄이는데 도움이 될지 모델링을 해봐야, 학습을 시켜봐야 알 수 있음
➜ 뭐가 얼마나 도움이 될지 알 수 없음 + 도움 되던 것이 다른 걸 만들었을 땐 도움 안될 수도
➜ 충분한 개수의 특징을 제작했는지 알 수 없음. 사람이 찾지 못한 요인들이 있을 수 있음
➜ 그만큼 모델을 많이 만들어야 했고, 설명은 지저분해짐 + 어려움
➜ 주어진 데이터가 얼마나 '적절'한지에 따라 의사결정 rule 제작의 난이도가 다르다.
➜ feature engineering: 주어진 데이터를, 의사결정에 도움되도록 더 적절히 만들어보는 절차
딥러닝: feature의 '양'과 '학습 수준'만 결정하면 모델이 좋은 feature를 알아서 결정해준다.
( feature의 양: 노드의 개수 )
( feature의 학습수준: 히든 레이어의 개수 )
(공간만 만들어주면 예측에 도움이 되도록, 오차가 줄어드는 방향으로 좋은 특징들을 알아서 만들어준다)
➜ feature engineering을 알아서 한다는 것
좋은 feature란?
➜ Error를 줄여줌 (예측력 상승)
➜ 설명이 용이함
➜ 모델링하기에 충분히 많은 데이터
딥러닝의 학습
학습: 오차를 줄이는 방향으로 가중치를 업데이트하는 것
(z함수 - 성능상 유용 + 설명상 유용)
딥러닝은 모델이 스스로 성능에 유용한 feature를 알아서 만든 것
➜ 그러나 딥러닝에서는 설명상 유용하지 않음 (히든 레이어 때문에)
➜ 그래서 성능에 몰빵
어떻게든 유용할 것이라고 판단한 피처를 만들어 내 성능이라도 올려보잔 마인드
(지도 학습이고 에러는 정의할 수 있으니 에러는 줄여보자)
각 히든 레이어에서 더 유용한 feature를 생성하여 다음 히든 레이어에 넣음
(high-level의 feature 생성)
ex) Dense(32)
➜ 히든 레이어 속 32개의 노드는 즉, 유용한 32개의 기존에 없던 새로운 feature를 만든다는 의미
➜ 첫 번째 히든레이어의 노드 수는 Input으로부터 새롭게 추출된 feature 개수
(층이 깊어질수록 더 고수준, 추상적)
(* 히든 레이어가 너무 고수준이면 기울기가 소실 -> vanish gradient)
딥러닝의 이러한 과정을
Feature Representation이라고 한다
: 연결된 것으로부터 기존에 없던 새로운 특징을 추출.
Q1. 만약 첫번째 히든 레이어에 노드를 1개 추가, 모델 성능이 증가하였다 그 이유는?
➜ 성능에 유용한 feature를 새롭게 생성했으므로 성능이 증가.
Q2. 만약 두 번째 히든 레이어에서 노드 1개를 삭제, 모델 성능이 유지되었다 그 이유는?
➜ 삭제된 노드는 성능에 큰 영향을 주는 feature가 아니었다.
(상대적으로 고수준인 두번째 레이어가 불필요했다는 의미와 동일)
Q3. 세 번째 히든 레이어를 추가하였더니 성능이 증가했다. 그 이유는?
➜ 구체적으로 어떤 feature가 필요한 것인지는 딥러닝 모델의 설명이 불가능한 특징 때문에 알 수는 없지만
좀 더 고수준의 feature가 필요한 상황이라는 방증
Q4. 모델이 학습이 잘 된 상황이라면 레이어와 레이어 안 노드는 몇 개가 적당한지 어떻게 알 수 있는가?
(특징 수준, 특징 개수)
➜ 모델에 공간(특징이 만들어지는)만 설정해주면 모델이 알아서 찾아준다.
(머신러닝과 딥러닝의 가장 큰 차이 중 하나)
성능 향상이 없을 때까지 노드를 늘려보세요.
그러고 나서 하이퍼 파라미터 튜닝을 시도해보세요.
- 요슈아 벤지오

<요약>
히든 레이어의 수: 내가 추출하고자 하는 feature의 수준(level)
노드(feature)의 수: 이전 레이어로부터 추출된 feature
연결된 것으로부터 기존에 없던 새로운 특징을 만들어내는 과정 (feature representation)
딥러닝이 강한 분야
- Tabular Data가 아닌 데이터를 사용하는 분야
(Tabular Data 이미 잘 정제된, 데이터가 크지 않고, 사람이 feature engineering을 할만한 데이터)
➜ Tabular Data에서는 머신러닝이 딥러닝보다 성능이 좋거나 비슷하다.
- 수작업이 힘든 데이터
➜ feature engineering이 너무 힘든 데이터 (영상 데이터, 자연어 데이터 등)
➜ 다양한 형태의 데이터를 다루는 분야
Chapter 2. 선형 회귀 (Linear Regression)
데이터를 가장 잘 설명할 수 있는 선을 찾는 방법

- 기울기 a, 절편 b에 따라 선의 모양이 정해짐.
- 선형 회귀 분석의 목적 또한 데이터를 가장 잘 설명할 수 있는 a와 b를 찾는 것.
- 선은 실제 데이터와 차이가 발생 ➜ 손실(Loss)
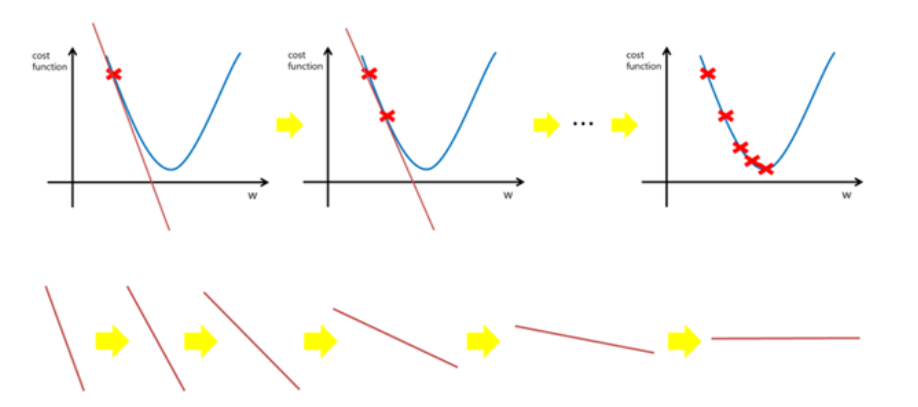
경사하강법 (Gradient Descent) 기초

- 손실을 최소화하기 위한 방법.
- 파라미터를 임의로 정한 다음 조금씩 변화시켜가며 손실을 점점 줄여가는 방법으로 최적의 파라미터를 찾아나감
- 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 극값(최적값)에 이를 때까지 반복하는 것
- 파라미터(기울기&절편)를 계속 조절하다보면 최적의 값으로 수렴함
- 학습률(learning rate)을 작게 설정하면 최적값으로 수렴할 때까지 시간이 오래 걸림
- 미분 값(기울기)이 최소가 되는 점을 찾아 알맞은 weight(가중치 매개변수)를 찾아냄
옵티마이저 (Optimizer, 최적화)
옵티마이저: GD(Gradoemt Descent)를 기본으로 하여 loss function이 최소가 되는 지점, 즉 최적의 가중치를 찾는 방법
➜ 경사 하강법 처리 방법
오차수정
➜ 잘못 그은 선 바로 잡기
(일단 선을 그리고 조금씩 수정해 나가기)
(오차가 최소가 될 때까지)


기울기 a와 오차와의 관계
: 적절한 기울기를 찾았을 때 오차가 최소화됨

- 해당 함수의 최소값 위치를 찾기 위해 비용함수(Cost Function)의 경사 반대 방향으로 정의한 step size를 가지고 조금씩 움직여 가면서 최적의 파라미터를 찾으려는 방법.
- 여기서 경사는 파라미터에 대해 편미분한 벡터를 의미.
- 이 파라미터를 반복적으로 조금씩 움직이는 것이 관건.
➜ 모델을 학습 시킬 때 최적의 학습률을 찾는 것이 중요
(효율적으로 파라미터를 조정하면서 결국 최적의 값을 찾아 수렴할 수 있을 수준으로!)
(학습률: 얼만큼 이동시킬지 이동 거리를 정해주는 것)

학습률이 너무 작을 경우, (step size가 작을 수록)
➜ 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습시간이 오래걸림.
➜ 지역 최소값(local minimum)에 수렴할 수 있음.
학습률이 너무 클 경우, (step size가 클수록)
➜ 학습 시간은 적게 걸림.
➜ 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최소값에서 멀어질 수 있음.
<요약>
학습률: (어느만큼 이동시킬지를 신중히 결정해야 하는데,이때) 이동거리를정해주는것
경사하강법: 오차의 변화에 따라 이차함수 그래프를 만들고 적절한 학습률을 설정해 미분값이 0인 지점을 구하는것
경사하강법 (Gradient Descent) 심화
경사하강법 진행순서

1 단계: w1에 대한 시작점 선택하는 것.
- linear regression의 경우 위의 그림과 같이 매끈한 모양으로 시작점은 별로 중요하지 않다.
- 많은 경우, w1을 0으로 설정하거나 임의의 값을 선택.
- cost 함수가 위와 같지 않다면 시작값을 찾는 것이 매우 중요!
2 단계: 시작점에서 손실 곡선의 기울기(Gradient) 계산
- 기울기 = 편미분의 벡터 : 어느방향이 더 정확한지 혹은 더 부정확한지 알려줌.
- 단일 가중치에 대한 손실의 기울기 = 미분값
- 손실함수 곡선의 다음 지점을 결정하기 위해 경사하강법 알고리즘은 단일 가중의 일부를 시작점에 더함.
(어느 방향(+, -)으로 이동해야 하는지를 결정함)
- 기울기의 보폭(Learning rate, 학습률)을 통해 손실 곡선의 다음 지점으로 이동.
3단계: 위의 과정을 반복해 최소값에 점점 접근함.
* 경사하강법의 문제점
- 경사하강법은 현재 위치에서 기울기를 사용하기 때문에 지역 최소값에 빠질 수 있음.
- 무작위 초기화(random initialization)로 인해 알고리즘이 전역 최소값이 아닌 지역 최소값에 수렴할 수 있음.
- 평탄한 지역을 지나기 위해 시간이 오래 걸리고 일찍 멈추어서 전역 최소값에 도달하지 못할 수 있음.
* 해결방법: 모멘텀 (Momentum)
➜ 기울기에 관성을 부과하여 작은 기울기는 쉽게 넘어갈 수 있도록 만든 것.
ex) 언덕에서 공을 굴렸을 때 낮은 언덕(기울기가 완만한)은 공의 관성을 이용하여 쉽게 넘어갈 수 있게 하여
지역 최소값을 탈출할 수 있게 한다는 뜻.
배치 사이즈 (Batch Size)
Batch: 경사하강법에서 배치는 단일 반복에서 기울기를 계산하는 데 사용하는 data의 총 개수.
(경사하강법에서의 배치는 전체 데이터 셋이라고 가정)
➜ 연산 한번에 들어가는 데이터의 크기
배치 사이즈가 너무 큰 경우
: 한번에 처리해야 할 데이터의 양이 많아지므로 학습 속도가 느려지고, 메모리 부족 문제가 발생할 위험이 있음.
배치 사이즈가 너무 작은 경우
: 적은 데이터를 대상으로 가중치를 업데이트하고 이 업데이트가 자주 발생 ➜ 훈련이 불안정해짐.

확률적 경사 하강법 (SGD, Stochastic Grandient Descent)
경사하강법은 전체 데이터를 모두 사용해 기울기를 계산(Batch Gradient Descent)
➜ 학습하는데 많은 시간이 필요함
(10만개의 데이터가 있을 때, 데이터에 업데이트가 있을 때마다 10만번의 계산을 해야함)
스토캐스틱 경사하강법
매 step에서 딱 한개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 기울기 계산.
➜ 배치 크기가 1인 경사하강법
특징
- 매우 적은 데이터를 처리하기에 학습 속도가 빠름.
- 하나의 샘플만 메모리에 있으면 되기 때문에 큰 데이터셋도 학습 가능.
- Cost Function이 매우 불규칙할 경우, 알고리즘이 local minimum을 건너뛰도록 도와줌
➜ global minimum을 찾을 가능성이 높음.
샘플의 선택이 확률적(Stochastic)이기 때문에 배치 경사 하강법에 비해 불안정.
cost funciton이 local minimum에 이를 때까지 부드럽게 감소하지 않고 위아래로 요동치며 평균적으로 감소.
반복이 충분하면 SGD가 효과 있지만 노이즈가 매우 심함.
SGD의 여러 변형 함수의 최저점에 가까운 점을 찾을 가능성이 높지만 항상 보장되지는 않음.

미니 배치 경사 하강법 (Mini-Batch Gradient Descent)
미니 배치 경사 하강법은 배치 크기를 줄이고, 확률적 경사 하강법을 사용.
ex) 학습 데이터가 1000개이고, batch size를 100으로 잡았다고 할 때 총 10개의 mini batch가 나옴.
이 mini batch 하나당 한번씩 SGD 진행하므로 1 epoch당 총 10번의 SGD 진행한다고 할 수 있음.
전체 데이터셋을 대상으로 한 SGD보다 파라미터 공간에서 shooting이 줄어들게 되는데,
이는 한 미니 배치의 손실값 평균에 대해 경사 하강을 진행하기 때문.
Mini-Batch는 최적해에 더 가까이 도달할 수 있으나, Local optima 현상이 발생할 수 있음.
local optima 해결방법
: 학습 속도가 빠른 SGD의 장점을 사용하여 학습량 늘림.
Chapter 3. 다중 분류 (Multi-Class Classification)
로지스틱 회귀 (Logistic Regression)
- 이름은 회귀이지만, 분류 모델
- 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측
- 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘.

z = a * (Weight) + b * (Lengthb) + c * (Diagonal) + d * (Height) + e * (Widthb) + f
(a, b, c, d : 가중치 혹은 계수)
z : 어떠한 값도 가능하지만 확률이 되려면 0~1 사이의 값이 되어야 함.
z가 아주 큰 음수일 때 0이 되고, z가 아주 큰 양수일 때 1이 되도록 바꾸는 방법
➜ 시그모이드 (로지스틱 함수)
Sigmoid (Sigmoid Function, Logistic Function)

시그모이드는 로지스틱 함수의 한 종류로 신경망에서 자주 이용하는 활성화 함수
로지스틱 회귀분석 또는 Neural network의 Binary classification(이진분류) 마지막 레이어의 활성함수로 사용하는 함수.
sigmoid의 의미
➜ 선형식(z)의 값을 0~1 사이의 값으로 y를 만들어준다
z 입력에 무엇이 들어가든 함수값이 (0,1)로 제한됨.
(z가 작아질수록 y도 0에 가까워지며 작아진다. 중간값은 1/2)
(매우 큰 값을 가지면 함수값은 거의 1이며, 매우 작은 값을 가지면 거의 0임)
* 선형회귀와 Dense layer에서의 차이
Dense(1) : 선형 회귀
Dense(1, activation='sigmoid') : 로지스틱 회귀
단, Sigmoid는 input이 하나일 때 사용되는 함수
input이 여러 개일때도 사용할 수 있도록 일반화 한 함수는 SoftMax
(sigmoid의 대안 ➜ relu: relu에도 한계는 존재 ➜ 대안: (리키 relu 등) ➜ 최신 대안(swish))
다중 분류 (3개 이상)

기본적인 분류 문제는 y=0일 때와 y=1일 때 2가지로 나누게 되지만
다중 분류 문제는 y=0 y=1 y=2 … y=n 까지 n+1개의 카테고리 분류를 다룸.
이진 분류와 모델을 만들고 훈련하는 방식은 동일.
EX) iris 데이터셋
- 여러 개(3개 이상)의 아웃풋에서 가장 확률이 높은 클래스를 고르는 것
범주형 변수들을 단순히 수치형 변수처럼 대할 수 없는 문제가 있음
➜ 각 클래스별로 로지스틱 회귀
crossentropy : 분류와 분류를 비교 (이진 분류라면 binary_crossentopy)
분류 문제를 풀 때는 조금 더 직관적으로 이해하기 위해 보조 지표를 사용
metrics = 'accuracy'
"One vs The Others"
"One vs Rest"
- 앤드류 응(Andrew Ng) (코세라 창시자)
Softmax (SoftMax Function)
세 개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화 함수.
소프트맥스 함수의 출력 값을 확률 분포의 일부로 해석 가능
ex) 분류될 클래스가 n개라 할 때, n 차원의 벡터를 입력받아, 각 클래스에 속할 확률을 추정
➜ 출력 값의 총합이 1이 되는 특징을 가진 활성화 함수
➜ 가장 높은 확률 값을 찾아줌 (부드럽게)
activation='softmax'
원-핫 인코딩 (One-Hot Encoding)
One Hot Encoding (*one hot -> 혼자만 1)
(*one cold encoding)
데이터를 수많은 0과 한 개의 1의 값으로 데이터를 구별하는 인코딩
(0으로 이루어진 벡터에 단 한 개의 1의 값으로 해당 데이터의 값을 구별하는 것.)

➜ feature를 각 클래스에 맞춰 세분화
라이브러리: from tensor flow.keras.utils import to_categorical
Chapter 4. 딥러닝 모델링
교차 검증을 잘 사용하지 않고 검증 세트를 별도로 덜어내서 사용함.
➜ 딥러닝 분야의 데이터셋은 충분히 크기 때문에 검증 점수가 안정적임.
➜ 교차 검증을 수행하기에는 훈련 시간이 너무 오래 걸림
<sequential API 모델링 기본 과정>
<functional API 모델링 기본 과정>
(functional API : 엮을 레이어를 조절할 수 있다)
에폭 (Epoch)
훈련 데이터셋에 포함된 모든 데이터들이 한 번씩 모델을 통과한 횟수로, 모든 학습 데이터셋을 학습하는 횟수
1 epoch
: 전체 학습 데이터셋이 한 신경망에 적용되어 순전파와 역전파를 통해 신경망을 한번 통과했다는 의미.
epoch를 높일수록, 다양한 무작위 가중치로 학습을 해보는 것이므로 적합한 파라미터를 찾을 확률이 올라감.
➜ 손실값이 내려감.
단, 지나치게 epoch를 높이게 되면,
그 학습 데이터셋에 과적합(overfitting)되어 다른 데이터에 대해선 제대로 된 예측을 하지 못할 수 있음.
Overfitting & Underfitting
에포크 과대 적합
➜ 에포크 횟수가 많으면 훈련된 모델은 훈련 세트에 너무 잘 맞아 테스트 세트에는 오히려 점수가 나쁜 과대적합 모델
에포크 과소 적합
➜ 에포크 횟수가 적으면 훈련된 모델은 훈련 세트와 테스트 세트에 잘 맞지 않은 과소적합된 모델
훈련 세트 정확도는 에포크가 진행될수록 꾸준히 증가하는 반면, 테스트 세트 점수는 어느 순간 감소하기 시작함.

과대적합이 시작하기 전에 훈련을 멈추는 것을 조기 종료(early stopping)라고 함.
Early Stoping
Early Stopping ➜ 과적합 방지
* min_delta: 설정값보다 {monitor}의 값이 크게 개선되지 않으면 무의미한 것으로 처리
그렇다면, 적당한 히든 레이어와 노드의 수, 에폭 수는 어떻게 찾을까
➜ 요수아 벤지오 "성능이 최대한으로 개선될 때까지 해보기"
➜ 관습적으로는 2의 배수로 설정
➜ 해봐야 하는 것이므로 경험이 바탕이 된 통찰이 중요
Tip)
- 항상 x.shape, y.shape 모델 구조를 항상 확인하는 습관 가지기
- 배치 크기는 총 학습 데이터셋의 크기를 배치 크기로 나눴을 때, 딱 떨어지는 크기로 하는 것이 좋음.
(총 학습 데이터 셋이 10050개, 배치 크기를 1000개로 나누고 싶은 경우, 나머지인 50개를 무작위로 선택하여 버림)
참고
https://keras.io/ko/callbacks/
Callbacks - Keras Documentation
Usage of callbacks 콜백은 학습 과정의 특정 단계에서 적용할 함수의 세트입니다. 학습 과정 중 콜백을 사용해서 모델의 내적 상태와 통계자료를 확인 할 수 있습니다. 콜백의 리스트는 (키워드 인수
keras.io
https://velog.io/@arittung/DeepLearningStudyDay8
경사하강법(Grandient Descent) & 확률적 경사 하강법(SSD) & 미니 배치 경사 하강법 & 손실 함수
경사하강법 - step size, 진행 순서, 문제점과 해결방법, 배치 사이즈 / 확률적 경사하강법 - 특징, 에포크 / 미니 배치 경사 하강법 / 손실함수 - 평균제곱오차와 크로스엔트로피, 로지스틱 손실함수
velog.io