[모델링심화] 1. 성능
Chapter 0. 선 요약
성능 튜닝
1. 선형 모델
변수가 많을 수록 복잡한 모델
변수 선택법으로 AIC가 제일 작은 변수조합의 모델을 찾기
AIC = - 적합도 + 복잡도
(AIC 값으로 판단하는 모델은 선형모델, 로지스틱 회귀, 시계열)
2. 하이퍼파라미터 튜닝
Random Search : 주어진 범위 내에서, 지정된 횟수 만큼 무작위로 시도
Grid Search : 주어진 범위 내에서, 모든 조합을 시도
3. 튜닝 시 주의할 점
주어진 데이터에서 최고의 성능을 얻었을 지라도, 운영환경에서 그 성능이 보장되지 않을 수 있다.
(데이터는 계속 변해간다) (너무 미세하게 조정할 필요 없다)
모델링의 목표 : 적절한 복잡도 + 적절한 예측력
일반화 성능
1. 성능
Variance(성능의 편차)와 Bias(오차) 를 줄여야 한다
2. 성능의 평균으로 계산 ➔ 들쑥날쑥한 성능
Variance에 대처하는 우리의 자세 ➔ 여러 번 측정하고 성능의 평균 계산하기
무작위 실험
K-fold Cross Validation
3. 데이터 늘리기
학습용 데이터를 늘리면 ➔ Variance(성능의 편차)와 Bias(오차) 를 동시에 향상
그렇다고 데이터가 많으면 많을수록 좋기만 할까?
➔ 적절한 데이터의 크기가 있다! (Learning Curve)
모델 복잡도와 과적합
1. 모델의 복잡도
학습용 데이터에 있는 패턴을 모델에 반영한 정도
가장 단순한 모델 : 학습용 데이터에서 Y 값의 평균으로 예측하는 모델
가장 복잡한 모델 : 학습용 데이터에만 존재하는 독특한 패턴까지 모두 반영한 모델
2. 과적합 (Overfitting)
모델이 복잡할 수록, train set에 있는 독특한 패턴이 모델에 반영될 수록 Train set에 대한 성능은 엄청 좋아지지만,
다른 데이터(validation, test, 운영data)에서의 성능은 오히려 떨어지게 됨
➔ 이런 현상을 과적합이라고 함
해결책
하이퍼파라미터가 주로 모델의 복잡도에 영향을 줌
하이퍼파라미터 튜닝을 통해 해결 가능. (Grid Search, Random Search)
그러나, 하이퍼파라미터의 변화에 따른 성능 추세 확인 필요!
우리는 완벽한 모델이 아닌, 적절한 모델을 찾아내야 한다.
Chapter 1. 성능 튜닝
선형 모델 : 변수 선택법
선형 모델(선형회귀, 로지스틱 회귀) 의 성능
변수 선택에 따라 성능에 차이가 발생됨 (당연하지)
변수 선택법 : 전진선택법 (혹은, 후진 소거법)
AIC 값이 가장 작은 모델을 단계별, 순차적으로 탐색
Step ①: feature 별로 각각 단순회귀 모델을 생성하고 AIC 값 비교하여 제일 작은 변수 선정
Step ②: ①에서 선정된 변수 + 나머지 변수 하나씩 추가해가며 AIC 값이 가장 작은 모델의 변수 선정
(단, ① 보다 AIC가 더 낮아져야 함)
Step ③: 더 이상 AIC가 낮아지지 않을 때 까지 ②를 반복함.
후진 소거법은 전진선택법의 반대로 진행
(후진소거법: 일단 다 집어넣고 하나씩 빼기)
선형 모델 : AIC (Akaike information criterion)
모델의 적합도
모델이 train set을 얼마나 잘 설명하는지는 매우 중요합니다
그러나 모델이 과적합 되지 않도록 해야 합니다.
그래서 선형 모델에서의 적합도와, feature가 과도하게 늘어나는 것을 방지하도록 설계된 통계량이 AIC 입니다.
AIC(아카이케 통계량)
값이 작을 수록 좋은 모델
AIC = ( - 모델의 적합도, 설명력 + 변수의 개수 )
( 변수의 개수를 늘어날 때마다 AIC가 작아지다가,
어느 순간부터 적합도(설명력)이 늘어나는 것보다 변수의 개수가 더 영향을 줌) (U자형 그래프)
( AIC값이 가장 낮아지는 변수의 조합을 찾아내는 것이 AIC를 이용한 변수선택방법)
Hyperparameter Tuning
파라미터: 가중치
하이퍼파라미터: 머신러닝에서 인간이 개입할 여지
알고리즘을 이용하여 모델링할 때, 최적화하기 위한 파라미터
하이퍼 파리미터 튜닝을 통해 성능이 달라집니다
튜닝 하는 방법에 정답이 없습니다.
지식과 경험 + 다양한 시도(실험)
다양한 시도를 쉽게 만들어 줄 방법 2가지
1) Grid Search
2) Random Search
Grid Search Vs. Random Search

➔ 튜닝은 결국, 여러번 반복해서 제일 좋은 놈 찾기 (노가다)
1 . Random Search
1) 범위지정
딕셔너리{ }로 값 범위 지정
미지정 하이퍼 파라미터는 기본값으로 지정됨
2) 함수 불러오기
RandomizedSearchCV
3) 모델선언
(1) 기본모델 선언 (기본모델이 반드시 필요)
(2) Random Search 모델 선언
4) 학습
기본모델이 아니라 random search 모델로 학습
'params': 어떻게 시도한 건지 보여주는 부분
'mean_test_score': 시도한 것에 대한 성능
5) 예측 및 평가
.predict 시, random search모델로 사용하는데, 이 모델에는 k값 만큼의 모델이 들어있다.
그 중 가장 좋은 성능을 가진 모델로 알아서 예측 및 평가를 진행한다 (.best_score)
2. Grid Search
Random Search와 절차는 동일
차이점
1) 함수가 다르다. GridSearchCV
2) 지정된 범위에 대해서 전부 수행하고 최적의 하이퍼 파라미터를 찾아 줌
Random Search + Grid Search 적용 사례
➔ 하이퍼 파라미터 값을 어떻게 정해야 할지 경험이 없을 때,
➔ Random Search와 Grid Search를 함께 사용하기
(Random으로 먼저 가까운 값을 찾고, Grid로 좀 더 자세하게 찾기)
Hyperparameter Tuning시 주의할 점
파라미터의 세밀한 조정으로 최적화된 성능을 얻더라도 운영환경에서 성능이 보장되지 않는다.
1) Overfitting 될 수 있다.
2) 미래에 발생될 데이터는 과거와 다를 수 있다.
(시간이 지나면, 데이터는 달라진다) (현재의 모델은 미래의 데이터에는 적합하지 않을 수 있다.)
모델링의 목표
1) 완벽한적절한 예측력을 얻기 위해
2) 적절한 복잡도의 모델을 생성.
Chapter 2. 일반화 성능
일반화 성능
1. 모델링의 목표
모든 데이터 셋은 모집단의 부분집합
Training Set역시 모집단의 부분집합 (표본은 모집단의 부분집합)
모델링의 목표는
부분집합을 학습해서 모집단(모집단의 다른 부분집합)을 적절히 예측하는 것.
(적절한 성능을 얻는 것)
2. 성능 향상을 위한 노력

<믿을 만한 성능얻기>
- 편차 줄이기
① 성능의 평균으로 계산 ➔ 들쑥날쑥한 성능을 평균내어 계산 (성능은 평균으로 판단)
② 데이터 늘리기 ➔ Variance 감소시킴 (수집할 수 없다면 증식)
<성능 높이기>
- 오차 줄이기
① 데이터 늘리기 ➔ Bias 감소시킴
② 튜닝하기 ➔ Bais 감소, 과적합 피하기
1) 성능의 평균으로 평가하기
방법1: 여러 번 반복실행 (평균성능)

방법2: k-fold cross validation (k겹 교차검증)
모든 데이터가 한번씩은 Validation 용으로 사용되도록
데이터를 k 등분해서 k번 수행하고 평균 성능으로 평가

2) 데이터 늘리기
학습용 데이터의 양과 성능
Training Set의 크기가 커지면(데이터가 많으면) 모델 성능이 향상됨
이를 보여주는 그래프가 Learning Curves

데이터가 많을수록 항상 좋은가?
데이터가 많을 수록 성능이 개선되다가 어느 지점부터 성능 향상도가 꺾인다.
꺾인 이후는 데이터 증가에 따라 성능개선 효과는 급격히 줄어든다.
그런데, 데이터가 많은 만큼, 모델링 속도는 늦어진다. (데이터는 적당히 많아야 한다) (오캄의 면도날)
적절한 데이터 크기를 찾는 방법 : Elbow Method
Elbow Method
팔꿈치 지점 근방이 적절한 값
Trade-Off 관계일 때, 적절한 지점을 찾기 위한 휴리스틱 방법.

Chapter 3. 모델 복잡도와 과적합
과소적합과 과대적합

단순한 모델 vs 복잡한 모델
단순한 모델
➔ 대충, 적당히 학습한 모델
➔ 가장 단순한 모델 : y의 평균으로 예측하는 모델
복잡한 모델
➔ 학습 데이터의 구석구석까지 모두 반영한 모델
➔ 가장 복잡한 모델 : Train set의 모든 패턴이 반영된 모델
적절한 모델은 어떻게?
모델의 복잡도 : 학습용 데이터의 패턴을 반영하는 정도
알고리즘 마다 이 복잡도를 조절할 수 있는 방법이 有
➔ 복잡도를 조금씩 조절해 가면서 Train error와 Validation error를 측정하고 비교
1) 선형모델의 복잡도
아래와 같은 선형 모델에서 파라미터(변수)가 추가될수록 수학식이 복잡
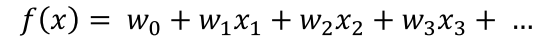
Training Set에 있는 속성(변수)를 많이 사용할 수록 Training Set에 대한 모델 정확도가 향상될 가능성이 높다.
(변수선택법)
2) 트리모델의 복잡도
크기에 영향을 주는 요소 : max depth, min samples leaf

3) SVM의 복잡도

모델의 복잡도와 과적합
적합도 그래프(Fitting Graph)
(Hold Out = Validation)

과적합 지점을 찾기 위한 단서 (공식적인 룰은 아니지만, 경험적인 이야기)
① train성능과 validation 성능이 급격히 벌어지는 지점
② validation 성능의 고점
③ 가능한 단순한 모델 (오캄의 면도날)
과적합이 문제되는 이유
➔ 모델이 복잡해 지면, 가짜 패턴(혹은 연관성)까지 학습하게 됨.
가짜 패턴
학습 데이터에만 존재하는 특이한 성질
모집단 전체의 특성은 아님 (학습데이터로 가짜패턴이 사용되면 성능에 악영향)
학습 데이터 이외의 데이터셋에서는 성능이 떨어진다
모델링 목적
학습용 데이터에 있는 패턴으로, 그 외 데이터(모집단 전체)를 적절히 예측
그러므로 학습한 패턴(모델)은, 학습용 데이터를 잘 설명할 뿐만 아니라, 다른 데이터도 잘 예측해야 한다
적절한 복잡도 → 적절한 예측력
TIP)
1. AIC
모델의 복잡도와 모델의 적합도를 적절하게 조절해주는 값
2. 우리는 완벽한 모델이 아닌, 적절한 모델을 찾아내야 한다.
3. 변수의 수는 모델의 복잡도를 결정한다.
4. 데이터는 적당히 많아야 한다.
5. 휴리스틱 법(heuristics) : 불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있게 보다 용이하게 구성된 간편추론의 방법
6. 모델의 최고성능은 적절한 복잡도에서