[모델링기초] 1. 선형회귀
Chapter 0. 선 요약
선형회귀 (Linear Regression)
1. 알고리즘의 원리 개념
➔ 선형회귀식(직선, 평면식)으로 Target과의 관계를 설명하는 모델
➔ 오차를 최소화해주는 선형회귀식을 찾는 최적화과정
2. 전제조건
➔ NaN 조치, 가변수화, feature들은 독립성 가정을 충족해야 함 (다중 공선성 문제 등)
3. 성능: hyper parameter, 복잡도 결정 요인
➔ 어떤 변수를 포함할 것인가? 즉, 선형회귀에서는 변수 선택이 가장 중요.
➔ 변수가 많을 수록 복잡해짐.
회귀모델 평가
1. 오차 비 : R-squared(평균모델 오차 대비, 회귀모델이 오차를 해결한 비율)
= 모델의 설명력, 결정계수 (최소값: -∞, 최대값: 1)
2. 오차의 양 : MSE, RMSE (오차 제곱의 평균), MAE(절대값 오차의 평균, 평균오차)
(제곱의 특징: 큰 것은 더 크게, 작은 것은 더 작게)
3. 오차의 율 : MAPE (오차율의 평균)
모델링은 데이터로부터 패턴을 찾아 수학식으로 정리하는 과정
Chapter 1. 모델링 개요
Model (모델)
데이터로부터 패턴(규칙, 반복)을 찾아 수학식으로 정리해 놓은 것
Modeling : 오차가 적은 모델, 오차를 최소화 시킨 모델을 만드는 과정
• 모델의 목적: 샘플을 가지고 전체를 추정, 예측, 추론
패턴을 찾는 2가지 방법
1) 답이 있는 상황에서 패턴 찾기 (정답有) ➔ 답(y)을 알려주면서 패턴을 찾음
= 지도학습(Supervised Learning)
• 답의 종류
(1) 숫자 ➔ 회귀 ex) 내일 코스피는 얼마일까?
(2) 범주 ➔ 분류 ex) 내일 코스피는 오를까? ('답이 Yes or No 라면' 분류 문제)
2) 답이 없는 상황에서 패턴 찾기 (정답無) ➔ 데이터 안에서 비슷한 것들끼리 묶어 패턴을 찾음
= 비지도 학습(Unsupervised Learning)
오차
실제 값 = 모델 + 오차
(모델 ➔ 찾아낸 패턴, signal)
(오차 ➔ 자료가 벗어난 정도(Sum of Square Error) = σ(실제값 − 모델)^2, noise)
모델링의 목표는 오차의 최소화 (모형이 실제를 설명하는 영역을 최대화)
평균
• 통계학에서 사용되는 가장 단순한 모형 중 하나
• 관측값과 모형의 차이: 이탈도(deviance)

모델링 예시
1. 데이터 로딩

우리의 비즈니스 목표: 광고비용 지출에 따른 매출액 예상
2. 데이터 전처리
1) 데이터를 X와 Y로 나누기

target = 'Sales'
x = data.drop(target, axis=1)
y = data.loc[:, target]2) train, val (test)로 분할 (학습용과 검증용)

# train : test의 비율을 7 : 3으로 나누기
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3) # 4덩이
3. 학습
1) 함수 불러오기
from sklearn.linear_model import LinearRegression #선형회귀
from sklearn.metrics import *2) 선언 (설계)
# 선형회귀(디폴트)를 model로 저장하여 사용
model = LinearRegression()3) 학습 (모델링)
# 학습용 데이터로 학습
model.fit(x_train, y_train)4) 검증
(1) 예측 (일종의 모의고사)
학습할 때 x 데이터 구조와 예측할 때 x의 구조는 똑같아야 함
# 테스트용 데이터(모의고사)로 모델이 얼마나 정확한지 검증
pred = model.predict(x_test)(2) 평가
# 정답지와 예측치를 비교
mean_absolute_error(y_test, pred) #평균오차>>> 1.3187794881015067
• 모델이 예측한 매출액과 실제값에는 1.3정도의 평균오차가 있었다.
Chapter 2. Linear Regression 1
단순회귀(Simple Regression)
➔ 하나의 예측변수로 하나의 결과변수를 예측
ex) <집값 예측 모델의 수학식>
집값 = -2 * (하위계층의 비율) + 10
: 하나의 예측변수(하위 계층의 비율)로 결과변수(집값)을 예측
➔ 자료를 설명하는 직선을 여러 개가 있을 수 있지만
그 중 가장 잘 데이터를 설명하는 하나의 직선, 직선식으로 요약 (전체 오차가 가장 적은 직선)
• 머신러닝이 직선을 찾는 방법
= 최적화 ➔ 기울기와 절편을 조절하여 오차를 조금씩 줄이며 직선을 찾아감
데이터 분할 (train, validation, test)

• train: 모델링에 사용되는 학습용 데이터
• validation (= val): train과 함께 모델링에 사용되는 검증용 데이터
• test: 데이터셋이 준비된 처음부터 떼어내는 부분
(마치 운영에서 발생된 데이터인양 간주)
(최종 검토용)
모델 내부 열어 보기
• 모델.coef_: 회귀계수 (=기울기)
• 모델.intercept_: y절편 (=가중치)
ex) <집값 예측 모델의 수학식>
집값 = (회귀계수) * (하위계층의 비율) + (y절편)
예를 들어, medv = -2 * (lstat) + 10에서 기울기가 나타내는 비즈니스적 의미는 (집값 단위: 1000달러)
➔ 하위비율이 1% 올라가면, 집값은 1000달러 하락
회귀 모델 평가
✓ 회귀 모델은 두 가지 관점으로 평가
1) [y의 평균] 모델의 오차 vs [회귀] 모델의 오차
➔ R² Score (=오차의비, 설명력, 결정계수)
2) [실제 값(y)] vs [회귀 모델의 예측 값(y)]
➔ MSE, RMSE, MAE, MAPE (=오차의 크기, 오차율)

1. 오차의 비로 평가하기: R²
① 평균모델과 실제값(Yi) 과의 차이(SST) ➔ (의미: 회귀모델에서 BaseLine이 되는 오차)
② 평균 모델과 회귀모델 과의 차이(SSR) ➔ (의미: 회귀모델로 예측할 때 발생하는 오차)
③ 실제 값과 회귀모델 과의 차이(SSE) ➔ (의미: 회귀모델이 기존모델(평균모델)에서 해결한 오차)


➔ 평균 모델의 오차 대비 회귀모델이 해결한 오차의 비율
➔ 회귀모델이 얼마나 오차를 해결(설명)했는지를 나타냄
➔ 결정계수, 모델의 설명력 이라고 부르기도 함.
*(SSE / SST = 잔차)
2. 오차의 양과 율로 비교하기

*(제곱의 특성: 큰 값은 더 크게, 작은 값은 더 작게 만들어줌)


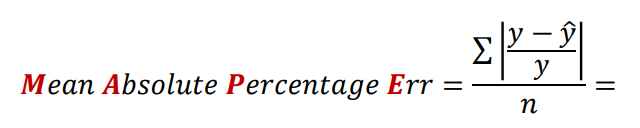
print("r2_score: ",r2_score(y_val,pred2))
print("MSE: ",mean_squared_error(y_val,pred2))
print("RMSE: ",mean_squared_error(y_val,pred2,squared=False))
print("MAE :",mean_absolute_error(y_val,pred2)) #평균오차
print("MAPE :",mean_absolute_percentage_error(y_val,pred2)) #평균오차율
print("회귀모델의 정확도 :",1-mean_absolute_percentage_error(y_val,pred2)) # 1 - MAPE: 회귀모델의 정확도*(Quiz)
평균오차율(MAPE)의 최대_최소값(범위)는?
➔ 0 ~ 100%가 아니다. (오차율은 무한대까지 훨씬 커질 수도 있음)
➔ 오차가 무한대에 가까워지면 회귀모델의 정확도도 마이너스로 갈 수 있음
*(정리)
(1) R² score: 평균모델의 오차 중에서 회귀 모델이 해결(설명)한 비율
(2) MSE: 오차 제곱의 평균
(3) RMSE: 오차 제곱의 평균의 제곱근 (큰 값은 더 크게, 작은 값은 더 작아짐)
(4) MAE: 평균오차
(5) MAPE: 평균오차율
Chapter 3. Linear Regression 2
다중회귀(Multiple Regression)
➔ 복수의 예측변수로 하나의 결과변수를 예측
➔ Feature가 2개 이상 (단, Feature들 간에 상관관계가 없이 독립적이어야 한다)
ex) <집값 예측 모델의 수학식>
집값 = -2 * (하위계층의 비율) + -1.3 * (범죄율) + 6 * (재산세율) 이라고 가정하면
'재산세율' 변수가 '하위계층의 비율' 변수보다 회귀모델에서 더 중요하다는 의미가 아닌 것
(단, 스케일링 과정이 있다면 더 중요한 변수의 의미를 뽑아낼 수 있음)
참조: 다중 공선성(Multi-Collinearity) - 변수들이 독립적이지 않을 때 생기는 문제
✓ 공선성(collinearity)
• 하나의 독립변수가 다른 하나의 독립변수로 잘 예측되는 경우, 또는 서로 상관이 높은 경우
ex) a 변수와 b 변수가 결과(Y)에 영향을 줄 때, a = 2 * b + 1 처럼 하나의 변수가 다른 변수로 예측이 됨
✓ 다중 공선성(multi-collinearity)
• 하나의 독립변수가 다른 여러 개의 독립변수들로 잘 예측되는 경우
✓ 다중 공선성이 있으면
• 회귀계수 추정이 잘 되지 않거나 불안정해져서 데이터가 약간만 바뀌어도 추정치가 크게 달라짐
• 계수가 통계적으로 유의미하지 않은 것처럼 나올 수 있음
ex) y = 3 * a - 2 * b + 5 일 때, a와 y의 관계는 3
그러나, b = 2 * a - 1로 표현이 되면 ➔ y = - 1 * a + 7로 회귀식이 바뀜
✓ 다중 공선성을 확인하기 위한 방법: 분산 팽창 지수(VIF, Variance Inflation Factor)
• 일반적으로 VIF 값이
• 5 이상 : 다중 공선성 존재
• 10 이상 : 강한 다중 공선성
• 공식 𝑉𝐼𝐹j = 1 1 − 𝑅j 2
(R² 이용)
✓ 그러나, 다중 공선성이 항상 성능에 문제가 되는 것은 아닐 수 있다.
• 실험을 해봐야 한다.
============================================================================================
Tip)
(1) X_train(행렬), y_train(벡터)은 개발자들이 가장 많이 쓰는 변수 이름
X를 굳이 대문자로 쓰는 이유: 행렬은 수학적으로 대문자로 쓰고, 벡터는 소문자로 쓰기 때문
(2) 파이썬에서 함수끝에 '_'가 붙으면 값을 나타냄
ex) model.coef_, model.intercept_